Índice
- Análise de dados para E-commerce
- Os dados e as probabilidades
- Combinação de dados
- Curva de Gauss, Distribuição Normal
- Distribuição normal em resultados de provas
- Princípio de Pareto
- O que diz a Lei de Benford?
- Exemplo da Lei de Benford
- Explicando a Lei Matemática de Benford
- Aplicações da Lei de Benford
- 10 aplicações práticas da Lei de Benford
E-book e Planilha para Calcular KPIs do E-commerce
Use os dados da sua loja virtual a seu favor e saia na frente da concorrência!
Na edrone, coletamos uma enorme quantidade de dados das mais de 1.000 lojas online que usam nossa plataforma. Entre estes dados estão valores aparentemente aleatórios, como os valores dos pedidos. Mas, na verdade, estes valores não são aleatórios.
Também conhecida como Lei do Primeiro Dígito, a Lei de Benford apresenta uma escala de proporção matemática que pode ser usada para análise de dados.
Em lojas virtuais, por exemplo, os dados são determinados pelos preços dos produtos, e segundo os princípios da Lei de Benford há uma probabilidade de 30% que o valor total do pedido terá o número “1” como primeiro dígito.
Nesse artigo vamos explicar como a matemática e as proporções numéricas podem afetar as análises de dados do e-commerce.
Análise de dados para E-commerce
Todo bom gestor de e-commerce confia em seus dados. Eles são necessários para embasar as decisões tomadas no dia a dia.
No entanto, as estatísticas nem sempre são a fonte de informações inequívocas que gostaríamos que fossem. Na verdade, elas até são, mas os problemas começam a surgir quando tentamos tratar os dados de forma determinante para tentar prever exatamente o que irá acontecer.
Isso é diferente de pensar que eles nos dão pistas sobre o que pode acontecer, com algum grau de certeza.
Os dados e as probabilidades
Tomemos um exemplo clássico de probabilidade – um dado comum de seis lados. Para simplificar, vamos chamá-lo de “D6”.
Quando jogamos o dado apenas uma vez, não temos ideia de qual valor entre 1 e 6 será obtido. Mas quando jogamos o dado 600.000 vezes, certamente teremos cerca de 100.000 ocorrências de cada valor.
Isso acontece porque a probabilidade dos resultados está distribuída igualmente, ou seja, cada face do dado tem as mesmas chances de ficar virada para cima.
Dados “D6” são um bom ponto de partida porque seus valores são totalmente aleatórios. Nada afeta os resultados. É claro, você pode burlar os resultados usando um dado viciado, mas este não é o caso aqui.
Já os valores de pedidos em lojas virtuais são outra história. Os valores parecem aleatórios mas, como já vimos, estão submetidos a algum tipo de predefinição. Algo parecido começa a acontecer quando usamos mais de um dado em cada jogada e anotamos os resultados.
Combinação de dados
À medida que adicionamos mais fatores, o efeito deixa de ser uma distribuição equivalente dos resultados. A soma dos valores dos dados estará distribuída em um intervalo de “2” a “12” mas, na maioria das jogadas, o resultado será “7”.
Isso é mais fácil de visualizar dispondo os resultados em uma tabela. O “7” tem uma chance maior de ser o resultado porque este valor pode ser obtido com duas combinações de “1” e “6”, duas combinações de “2” e “5”, e duas combinações de “3” e “4”. A distribuição, antes equilibrada, começa a se curvar.
Quanto mais dados adicionamos às jogadas, mais os resultados começam a tomar a forma de um sino. Aqui vemos a distribuição com três dados:
E aqui com quatro dados:
O último exemplo é muito parecido com a estrela da próxima seção — a distribuição normal.
Primeira conclusão: Coletando-se muitas amostras, é possível prever como os resultados agregados serão distribuídos.
Curva de Gauss, Distribuição Normal
Um dos aspectos elementares da estatística é a distribuição normal, ou Curva de Gauss, demonstrada pelo teorema central do limite.
O teorema central do limite afirma que, tendo-se uma população com mediana μ e desvio padrão σ, ao se tomar um número suficientemente grande de amostras desta população, a distribuição das amostras se aproximará da distribuição normal.
Em outras palavras, quando variáveis aleatórias e independentes (p. ex. jogadas de dados D6) se acumulam (como exemplificado pelo uso de mais de um dado), os resultados convergem rumo à distribuição normal.
O último exemplo mostra exatamente esta situação — os quatro dados D6 (fatores aleatórios e independentes) somam 1.296 resultados possíveis. Cada jogada individual é imprevisível, mas à medida que compilamos os resultados, a distribuição normal vai aparecendo.
Vamos discutir alguns exemplos da vida real.
Distribuição normal em resultados de provas
Os resultados do exame final do ensino médio polonês são um ótimo exemplo de como a distribuição normal funciona na prática… e uma demonstração inequívoca da intervenção dos avaliadores sobre as pontuações.
Os resultados deveriam seguir uma curva de Gauss padrão. O centro da curva pode estar um pouco mais para a direita caso a prova seja mais fácil (média das notas mais alta), ou para a esquerda caso seja mais difícil (média das notas mais baixa).
Na prática:
Há duas coisas interessantes aqui. A primeira é que a minha nota está em algum lugar deste gráfico. A segunda é a anomalia que ocorre perto da marca dos 20 pontos. Quer tentar adivinhar qual é a nota de corte do exame final na Polônia?
Nenhum dos professores avaliadores quer que seus alunos reprovem. Como este exame é decisivo para a continuidade dos estudos, ao observar que um estudante está a poucos pontos da nota de aprovação, o avaliador tenderá a ser um pouco mais generoso na pontuação.
Segunda conclusão: Com uma amostragem grande o suficiente, é possível verificar se os resultados foram manipulados.
No entanto, embora seja altamente improvável, é teoricamente possível que todos os estudantes obtenham nota máxima. O essencial aqui é que cada amostra (no caso, a prova de cada estudante) é independente. Se o estudante ganha ou perde pontos, isso não afeta os resultados dos outros estudantes.
Princípio de Pareto
A distribuição gaussiana parece se aplicar a coisas, de certa forma, inanimadas. O Princípio de Pareto, por outro lado, parece influenciar nossas decisões.
Esta distribuição também é conhecida como o Princípio de Pareto ou regra 80/20. Este último termo reflete bem como a distribuição se aplica na prática:
- 20% dos clientes geram 80% do faturamento de uma loja
- 20% dos empregados de uma loja fazem 80% de todo o “trabalho”
- 20% das ações de Marketing de um eCommerce trazem 80% dos resultados
E outras relações um pouco mais surpreendentes:
- 20% de um texto transmite 80% de toda a informação
- 80% da massa total de meteoritos que atingiram a Terra vieram de 20% das quedas
- 20% das maiores cidades abrigam 80% da população mundial.
Terceira conclusão: Com muitas amostras e conhecimento sobre os fenômenos, podemos identificar qual tipo de distribuição se aplica.
Aposte no conhecimento para desenvolver o seu negócio!
O que diz a Lei de Benford?
Agora que passamos por alguns conceitos básicos de estatística, finalmente podemos abordar o tema principal deste artigo.
Antes de mais nada, vale destacar que a Lei de Benford se aplica apenas a valores que passam por várias ordens de magnitude. Ou seja, se pegarmos uma série de valores em um intervalo de 1 a 10, não observaremos este fenômeno.
A Lei de Benford afirma que em ordens de grande magnitude, ou seja em uma grande escala numérica, o número 1 tem 30% mais chances de aparecer como primeiro dígito.
Se você não acredita, nós podemos provar!
Dê uma olhada na proporção entre os dígitos iniciais de uma contagem de pedidos do sistema edrone.
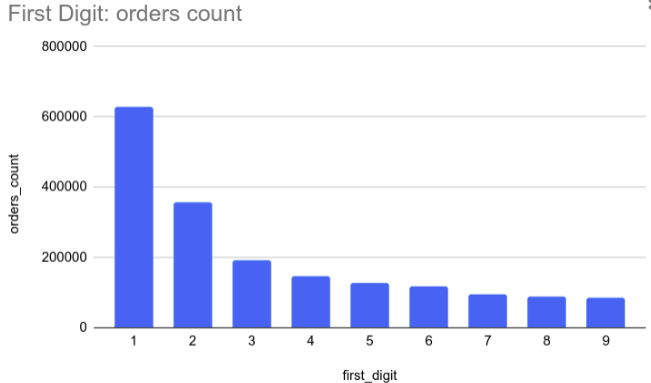
O gráfico acima é uma comprovação prática da Lei de Benford nos dados de uma loja virtual, mas ela não se aplica apenas ao e-commerce.
Veja a seguir outros exemplos da Lei de Benford.
Exemplo da Lei de Benford
O melhor exemplo prático da Lei de Benford envolve bilhetes de rifa.
Imagine que você está emitindo os bilhetes em uma sequência numérica e contando a probabilidade de pegar da pilha um bilhete que tenha o número “1” como primeiro dígito.
Nós começamos pelo primeiro bilhete, número “1”, e neste caso a probabilidade é 100%. Quando adicionamos o bilhete número “2”, a probabilidade cai para 50%. Ao adicionar o terceiro bilhete, a probabilidade cai para ~33%.
1 -> 1/1 = 100%
2 -> 1/2 = 50%
3 -> 1/3 = 33%
[…]
9 -> 1/9 = 11%
Quando chegamos a nove bilhetes, as chances do número do bilhete começar com “1” são de 11%, mas quando adicionamos o décimo bilhete, a probabilidade começa a subir:
10 -> 2/10 = 20%
11 -> 3/11 = 27%
12 -> 4/12 = 33%
13 -> 5/13 = 38%
[…]
19 -> 11/19 = 58%
Quando chegamos a 20 bilhetes, a probabilidade volta a cair gradualmente até atingirmos o centésimo bilhete. No intervalo de 100 a 199 bilhetes, as chances aumentam, caindo novamente no intervalo de 200 a 999. E assim por diante.
Como estamos lidando com potências de 10, as distâncias entre as “subidas” e “descidas” das probabilidades vão se tornando cada vez maiores. Se aplicarmos os dados a uma escala logarítmica, o gráfico vai se parecer mais ou menos como uma serra. Em vez de unidades, escala logarítmica usa potências de 10 como intervalos. Ou seja, em vez de “1, 2, 3, 4”, tem-se “1, 10, 100, 1000”.
Se continuarmos coletando as probabilidades até atingirmos um grande volume de amostras e depois calcularmos a média, chegaremos ao valor de 0.301 (30,1%).
Para calcular a probabilidade de cada número ser o primeiro dígito, podemos usar a seguinte equação:
[ {P(d)= log_{10} (1+1/d) } ]
Sendo d o dígito em questão.
Os resultados são:
1 -> 0.30103 (30,1%)
2 -> 0.17609 (17,6%)
3 -> 0.12494 (12,4%)
4 -> 0.09691 (9,6%)
5 -> 0.07918 (7,9%)
6 -> 0.06695 (6,6%)
7 -> 0.05799 (5,7%)
8 -> 0.05115 (5,1%)
9 -> 0.04576 (4,5%)
Explicando a Lei Matemática de Benford
Agora você vai entender o que já comprovamos: por que o número um aparece mais como primeiro dígito em grandes escalas numéricas?
Porque, quando começamos a contar uma sequência numérica, o ponto de partida é o um. Você precisa passar pelo “1” para chegar ao “7”, da mesma forma que precisa passar pelo “10” para chegar ao “40”, e passar pelo “100” para chegar ao “300”. Nada garante que o seu primeiro dígito será “1”.
Mas, se por algum motivo ele for “9”, haveria ao menos a possibilidade dele ser “1” pois, ao contar o que quer que seja que o “9” representa neste caso, a contagem necessariamente começaria por “1”.
Veja a seguir como aplicar a Lei de Benford em diferentes ocasiões.
Aplicações da Lei de Benford
Agora você deve estar se perguntando: “mas como aplicar a Lei de Benford no meu dia a dia?”
Este fenômeno pode ser observado em amostras grandes que passam por várias ordens de magnitude. Um exemplo perfeito seria a população das cidades ao redor do mundo, que também seguem o Princípio de Pareto.
Via de regra, se os valores de uma amostra passam por várias ordens de magnitude, provavelmente seguirão a Lei de Benford, especialmente se estiverem em uma distribuição assimétrica positiva (quando a mediana é menor que a média).
10 aplicações práticas da Lei de Benford
- Dados financeiros, contábeis, e de empréstimos
- Transações de cartão de crédito, saldos bancários, valores de ações
- PIBs nacionais, populações de cidades ao redor do mundo
- Valores de pedidos, estoque, transações, reembolsos
- Tecnologia da Informação (tamanhos de arquivos em computadores)
- Biologia (comprimentos de proteínas)
- Física (comprimentos de onda em espectroscopia atômica, tempo de vida de hádrons, perda de energia rotacional de pulsares, entre outros)
- Contabilidade e finança: detecção de fraudes fiscais
- Política: detecção de fraudes eleitorais
- Microeconomia: treinamento de percepções sobre aleatoriedade e probabilidade
Aposto que, a partir de agora, você verá números aparentemente aleatórios com outros olhos 😉 E a edrone pode te ajudar a usar esses dados em cenários de automação de marketing para melhorar o engajamento com os clientes da sua loja virtual!
Quer aumentar as suas vendas e construir um relacionamento com os seus clientes?
Pedro Paranhos
Margeting manager
edrone
Gerente de Marketing LATAM na edrone. Profissional de marketing full-stack interessado em tecnologia, história (passado e futuro), negócios e idiomas. Leitor de livros e entusiasta de cervejas artesanais.
E-book e Planilha para Calcular KPIs do E-commerce
Use os dados da sua loja virtual a seu favor e saia na frente da concorrência!